
Πολύ συχνά οι μαθητές και οι γονείς τους περιγράφουν ένα «αόρατο χέρι» που ανεβοκατεβάζει τις βάσεις των σχολών. Πάρα πολλοί δυσκολεύονται να κατανοήσουν ότι είναι οι ίδιοι οι μαθητές ( με την επίδοσή τους αλλά και τις επιλογές του μηχανογραφικού τους δελτίου ) αυτοί που καθορίζουν την πορεία των βάσεων.
- Υπάρχει νομοθεσία που προβλέπει τι συμβαίνει σε περιπτώσεις μαθητών με τις ίδιες βαθμολογίες αλλά για χάρη της απλοποίησης της περιγραφής θα μείνουμε στον παραπάνω ορισμό που καλύπτει σχεδόν την απόλυτη πλειοψηφία των περιπτώσεων.
Ποιοι όμως είναι οι παράγοντες που καθορίζουν τις βάσεις των σχολών ;
- Η περιγραφή του τρόπου με τον οποίο καταλήγουμε σε αυτό που αποκαλούμε «βάση εισαγωγής» θα γίνει μέσα από ένα απλό παράδειγμα, για την απλοποίηση του οποίου δεν θα προβληθούν περιπτώσεις ισοβαθμίας μαθητών , ειδικά μαθήματα κτλ .

Οι μαθητές “μπαίνουν σε σειρά” σύμφωνα με την βαθμολογία τους
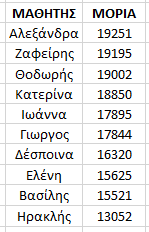
και καλούνται να δηλώσουν τις σχολές που επιθυμούν με σειρά προτίμησης (μηχανογραφικό σχολών) Για λόγους απλοποίησης της διαδικασίας παρουσιάζονται μέχρι 3 επιλογές τους .

Το σύστημα/πρόγραμμα απόδοσης σχολών αρχίζει να διαβάζει τις επιλογές τους ξεκινώντας από τον μαθητή με την υψηλότερη βαθμολογία “ικανοποιώντας” τις επιθυμίες τους εφόσον αυτό είναι δυνατόν .
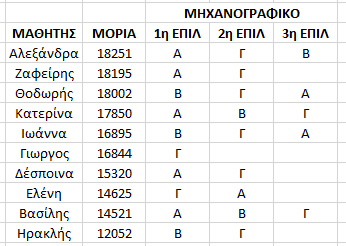
Ποιος το καθορίζει αυτό ? Μα το πλήθος των πρωτοετών φοιτητών που έχει δηλωθεί για κάθε σχολή ( Θυμίζω ότι στο παράδειγμά μας οι σχολές έχουν δηλώσει Α=2 , Β=3, Γ=3 )
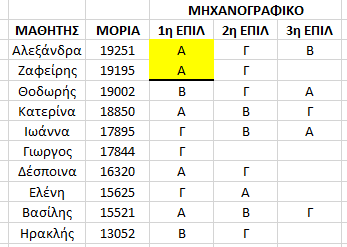
Φτάνοντας στον 2ο μαθητή η σχολή Α συμπληρώνει το πληθος μαθητών που μπορεί να δεχθεί και “κλειδώνει”.
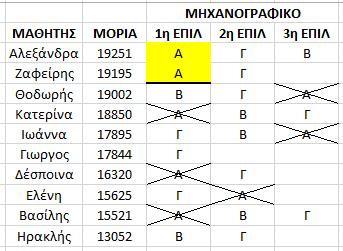
Ποιός είναι ο τελευταίος που μπήκε στην σχολή ; Ο Ζαφείρης με 19195 μόρια , άρα η “βάση” της σχολής Α είναι τα 19195 μόρια του. Η σχολή Α δεν είναι πλέον διαθέσιμη για τους υπόλοιπους που ακολουθούν ενώ το σύστημα συνεχίζει στον επόμενο μαθητή με σκοπό να του ικανοποιήσει την καλύτερη ( πλέον διαθέσιμη ) επιλογή του .
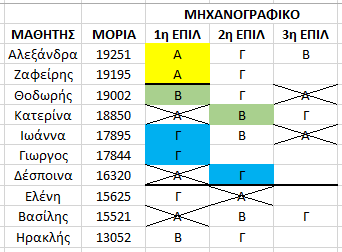
Στον 7ο μαθητή ( Δέσποινα ) συμπληρώνεται το πλήθος των μαθητών που μπορεί να δεχθεί η σχολή Γ ( βάση σχολής 16320 ) και δεν είναι πλέον διαθέσιμη για τους μαθητές που ακολουθούν.

Προσέξτε όμως τι συμβαίνει τώρα !!!
Ο 8ος μαθητής ( Ελένη ) παρόλο που έχει περισσότερα μόρια από τον 9ο ( Βασίλη ) μένει εκτός σχολών γιατί οι επιλογές του ήταν περιορισμένες και είχε την ατυχία να έχει τις ίδιες επιλογές σχολών με μαθητές που ήταν καλύτεροι από αυτόν ( και “πρόλαβαν” να του τις πάρουν ). Έτσι το “σύστημα απόδοσης σχολών” προσπερνά των 8ο μαθητή ( μιας που δεν έχει σχολή να του αποδόσει ) και πηγαίνει στον επόμενο.

ο οποίος παίρνει την τελευταία διαθέσιμη θέση της καλύτερης διαθέσιμης επιλογής σχολής που έχει κάνει. ( βάση σχολής Β : 15521 )
Οι μαθητές ήταν 10 ενώ οι διαθέσιμες θέσεις ήταν 8 ( 2+3+3 ), έτσι ξέραμε από την αρχή ότι 2 μαθητές θα μείνουν εκτός σχολών . Προσέξτε όμως !!! Ένας έμεινε εκτός γιατί είχε χαμηλή βαθμολογία ( Ηρακλής ) και το σύστημα δεν έφτασε καν σε αυτόν να τον ρωτήσει ενώ ένας μαθητής ( Ελένη ) έμεινε εκτός γιατί έκανε “λάθος” στο μηχανογραφικό και επέτρεψε στο σύστημα να την προσπεράσει χωρίς να της αποδώσει μια σχολή.
Τι θα συνέβαινε εάν όλοι οι μαθητές είχαν 1000 μόρια λιγότερα ( ή 1000 μόρια περισσότερα ) επειδή τα θέματα στις πανελλήνιες ήταν πιο δύσκολα ( ή πιο εύκολα )

Μα βέβαια δεν θα υπήρχε καμία διαφορά .Το σύστημα θα κατέληγε στην ίδια αρχική κατάταξη και ακολουθώντας την ίδια πορεία θα έκανε την ίδια απόδοση σχολών.
Να λοιπόν γιατί ακούτε την έκφραση ότι η δυσκολία ή η ευκολία των θεμάτων δεν έχει κάποια ιδιαίτερη σημασία. ΓΙΑΤΙ ΠΟΛΥ ΑΠΛΑ ΤΑ ΘΕΜΑΤΑ ΕΙΝΑΙ ΚΟΙΝΑ ΓΙΑ ΟΛΟΥΣ !!! Μπορεί να δώσουν στρεβλή κατάταξη ( συμπιέζοντας της επιδόσεις των μαθητών σε λίγα μόρια ή σε πολλά … αλλά αυτό είναι μια άλλη ιστορία )
- Αξίζει να ανοίξουμε μια μικρή παρένθεση όμως εδώ και να δούμε εάν η κατάταξη παραμένει ίδια με τα 1000 λιγότερα ( δύσκολα θέματα ) ή 1000 περισσότερα ( εύκολα θέματα ) μόρια . Ενώ η κατάταξη δεν διαφοροποιείται με 1000 μόρια λιγότερα , εάν τα θέματα είναι εύκολα υπάρχει διαφοροποίηση . Ποιός αδικείται ; Μα αυτός που δεν μπορεί να προσθέσει 1000 μόρια στο “σκορ” του. Δηλαδή η Αλεξάνδρα , ο Ζαφείρης και ο Θοδωρής δεν μπορούν να αποκτήσουν 20251 , 20195 και 20002 αντίστοιχα και εξισώνονται όλοι στα 20000 μόρια . Χρησιμοποιώντας λοιπόν “χημικούς όρους” , τα εύκολα θέματα εχουν ισοσταθμιστικό αποτέλεσμα ( Leveling effect ) μιας που οι διαφορές στις επιδόσεις των μαθητών εξαφανίζονται ή ισοσταθμίζονται. Αυτό σημαίνει ότι τα εύκολα θέματα ( ή καλύτερα τα θέματα χωρίς διαβάθμιση ) μειώνουν ( ή μηδενίζουν ) τις διαφορές στις βαθμολογίες μεταξύ των μαθητών και πιθανότατα ( εγώ θα έλεγα σίγουρα ) η τελική κατάταξη των μαθητών να μην αντικατοπτρίζει την πραγματική τους διαφορά στο διάβασμα και στην γενικότερη προσπάθεια που κατέβαλαν (ή στην εξυπνάδα τους, βρε αδελφέ). Το πόσο σημαντικό είναι αυτό θα φανεί στα αποτελέσματα του Αυγούστου.
Να λοιπόν γιατί οι μαθητές πρέπει να διαγωνίζονται στα ίδια μαθήματα και να γιατί δεν πρέπει να υπάρχουν κοινές σχολές στα ΕΠ. Γιατί πάρα πολύ απλά οι μαθητές αποκτούν το δικαίωμα εισαγωγής στις ίδιες σχολές ενώ έχουν διαγωνιστεί υπό διαφορετικούς όρους. Γιατί έχουν αποκτήσει με διαφορετικά κριτήρια ( θέματα ) το βαθμό πρόσβασης που θα τους βάλει στην ίδια κατάταξη επιλογής σχολών.
Έπρεπε να περάσουν τα 15 χρόνια του συστήματος Αρσένη για να το κατανοήσει αυτό η ελληνική οικογένεια και να απαιτήσει να αλλάξει. Ωστόσο όσο υπάρχουν κοινές σχολές στα ΕΠ το θέμα δεν έχει λυθεί πλήρως .
Τι θα συνέβαινε όμως εάν είχαμε διαφορετικά μηχανογραφικά . Ας κάνουμε μια πολύ πολύ μικρή αλλαγή στο μηχανογραφικό ενός μόνο μαθητή . Ας πούμε ότι η Αλεξάνδρα ( ο μαθητής με την μεγαλύτερη βαθμολογία ) δήλωνε ως 1η επιλογή την σχολή Γ και ως 2η την σχολή Α.

Ας ξανατρέξει το σύστημα/πρόγραμμα απόδοσης σχολών :
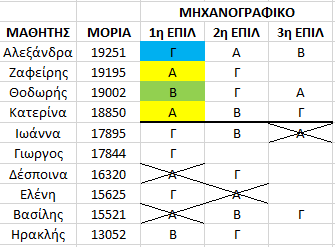
Η σχολή που κλειδώνει 1η είναι πάλι η Α αλλά αυτήν την φορά αυτό συμβαίνει στον 4ο μαθητή ( Κατερίνα ) και ως βάση της χαρακτηρίζονται τα 18850 μόριά του . Η απόδοση σχολών συνεχίζει δίνοντας στους μαθητές τις καλύτερες διαθέσιμες επιλογές τους. Η επόμενη σχολή που κλειδώνει ( και δεν είναι πλέον διαθέσιμη ) είναι η σχολή Γ και ως βάση της χαρακτηρίζεται ο βαθμός του τελευταίου εισακτέου σε αυτήν ( Γιώργος / βάση σχολής Γ : 17844 )

Η απόδοση σχολών συνεχίζει – προσπερνά την Δέσποινα και την Ελένη που οι σχολές που επιθυμούσαν είναι πλέον γεμάτες – και δίνει στον Βασίλη και στον Ηρακλή ( δύο μαθητές με χαμηλότερες βαθμολογίες ) την σχολή Β που είχε κενές θέσεις . ( βάση Β : 13052 μόρια )
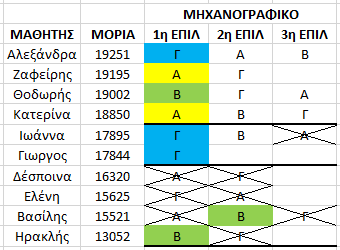
Προσέξτε πως η αλλαγή σε 1 μόνο σχολή έδωσε απέδωσε διαφορετικές σχολές στους μαθητές και πως άλλαξαν οι βάσεις των σχολών . ( η μεγάλη αυτή αλλαγή έγινε γιατί ο μαθητής που άλλαξε μηχανογραφικό ήταν 1ος στην προτεραιότητα … με λίγα λόγια πειράξαμε το 1ο “τουβλάκι” στο ντόμινο … αν αλλάζαμε το μηχανογραφικό του 4ου μαθητή η αλλαγή αυτή θα επηρέαζε ΜΟΝΟ τους μαθητές που θα είχαν μικρότερη βαθμολογία από αυτόν )
Νά λοιπόν τι είναι οι πανελλήνιες εξετάσεις !!! Είναι ένας διαγωνισμός στο οποίο ο κάθε μαθητής προσπαθεί να συγκεντρώσει το καλύτερο “σκορ” ώστε να μπορέσει να διαλέξει την σχολή που επιθυμεί χωρίς να το απασχολούν οι επιλογές των άλλων ή το πλήθος των θέσεων που προκηρύσσει κάθε σχολή .
Ας δούμε πως επηρεάζεται η απόδοση σχολών στους μαθητές εάν οι θέσεις στις σχολές ήταν διαφορετικές . Ας δούμε τι θα συνέβαινε εάν η σχολή Α δέχονταν 3 μαθητές , η σχολή Β δέχονταν 2 μαθητές και η σχολή Γ δέχονταν 3 μαθητές.
Κρατώντας τις ίδιες επιδόσεις μαθητών και το ίδιο μηχανογραφικό ( όπως στο 1ο παράδειγμα ) το πρόγραμμα απόδοσης σχολών αρχίζει ξανά να σαρώνει ξεκινώντας πάλι από τον μαθητή με την μεγαλύτερη βαθμολογία .
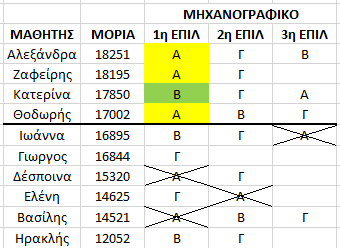
Βάση σχολής Α : 17002
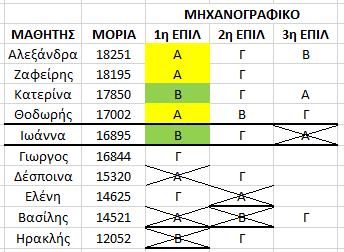
Βάση σχολής Β : 16895

Βάση σχολής Γ : 14625
Συμπέρασμα ( αντί επιλόγου )
Είναι φανερό ότι ο κάθε μαθητής δεν μπορεί να γνωρίζει ούτε το πλήθος των μαθητών που έχουν καλύτερη βαθμολογία από αυτόν αλλά ( κυρίως ) ούτε ποιές είναι οι επιλογές σχολών που έχουν κάνει αυτοί οι μαθητές , Για αυτόν τον λόγο πρέπει να κάνει μηχανογραφικό σαν να έχει το απόλυτο πλεονέκτημα δηλαδή 20000 μόρια. Δηλώνουμε όλες τις σχολές που μας ενδιαφέρουν σε όλες τις πόλεις που η οικογένεια μας μπορεί να υποστηρίξει οικονομικά τις σπουδές μας . Με αυτόν τον τρόπο ελαχιστοποιείται η πιθανότητα δυσάρεστων εκπλήξεων τον Αύγουστο.
Επιμέλεια άρθρου: Αντώνης Μπαλτζόπουλος-Χημικός
Πηγή : liveyourmaths.com/
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου